Multiples of 5 Understanding the Concept and Applications

When it comes to numbers, multiples play a significant role in various mathematical concepts and applications. One such important set of multiples is the multiples of 5. Multiples of 5 are numbers that can be evenly divided by 5 without leaving a remainder. Some examples of multiples of 5 include 15, 45, 35, 5, 30, 10, 20, and 40.

The concept of multiples of 5 is fundamental in arithmetic and helps in understanding various mathematical operations. For instance, when adding or subtracting multiples of 5, the result will always be a multiple of 5. This property makes multiples of 5 useful in mental calculations and estimation.

Furthermore, multiples of 5 are often encountered in real-life situations. For example, when counting money, the denominations of coins and bills often follow a pattern of multiples of 5. This makes it easier to count and organize money efficiently.

In addition, multiples of 5 are also important in measurement conversions. Many units of measurement, such as centimeters, inches, and feet, can be easily converted to multiples of 5, making it simpler to estimate and compare measurements.

Did you know? The concept of multiples of 5 extends beyond just numbers. In music, multiples of 5 are often used to create rhythmic patterns and time signatures. This adds a sense of structure and harmony to musical compositions.

In conclusion, understanding the concept of multiples of 5 is essential in mathematics and has practical applications in various fields. Whether it’s for mental calculations, counting money, or measurement conversions, multiples of 5 provide a foundation for efficient and accurate calculations.

What are Multiples of 5?

Multiples of 5 are numbers that can be evenly divided by 5. In other words, if a number can be multiplied by 5 to get a whole number, then it is a multiple of 5. For example, 25, 35, 40, 30, 10, 5, 15, and 45 are all multiples of 5.

When we say that a number is a multiple of 5, it means that it can be expressed as 5 times another number. For instance, 25 is a multiple of 5 because it can be written as 5 times 5. Similarly, 35 is a multiple of 5 because it can be written as 5 times 7.

Multiples of 5 have some interesting properties. For instance, all multiples of 5 end with either 0 or 5. This is because when we multiply any number by 5, the last digit of the product will always be 0 or 5. For example, 25, 35, and 40 all end with 5 or 0.

Understanding multiples of 5 is important in various mathematical concepts and applications. For example, when working with money, we often use multiples of 5 to calculate change or determine the total cost. Multiples of 5 are also used in measuring time, as there are 60 minutes in an hour and 12 hours in a day, both of which are multiples of 5.

In conclusion, multiples of 5 are numbers that can be evenly divided by 5. They have various properties and are used in many mathematical concepts and applications.

Definition and Examples

Multiples of 5 are numbers that can be divided evenly by 5. In other words, a multiple of 5 is any number that can be obtained by multiplying 5 by another whole number.

For example, 30 is a multiple of 5 because it can be divided evenly by 5 (30 ÷ 5 = 6). Similarly, 35 is a multiple of 5 because it can also be divided evenly by 5 (35 ÷ 5 = 7).

On the other hand, numbers like 25, 20, and 10 are also multiples of 5 because they can be obtained by multiplying 5 by 5, 4, and 2 respectively. For instance, 25 = 5 × 5, 20 = 5 × 4, and 10 = 5 × 2.

Furthermore, 40 and 45 are also multiples of 5 as they can be divided evenly by 5 (40 ÷ 5 = 8, 45 ÷ 5 = 9).

Understanding the concept of multiples of 5 is important in various applications, such as calculating time intervals, counting money, and solving problems involving patterns and sequences.

Properties and Patterns

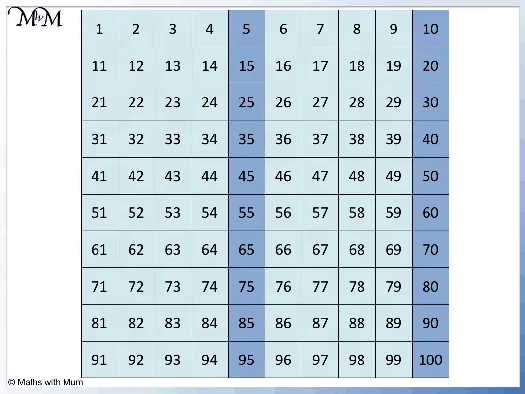
When working with multiples of 5, there are several properties and patterns that can be observed.

• The first property is that all multiples of 5 end with either 0 or 5. For example, 35, 10, 40, and 5 are all multiples of 5.
• Another property is that if a number is a multiple of 5, then its digits must add up to a multiple of 5 as well. For example, the digits of 45 add up to 9, which is not a multiple of 5. However, the digits of 25 add up to 7, which is also not a multiple of 5.
• One interesting pattern is that if you add any two multiples of 5 together, the result will always be a multiple of 5. For example, 20 and 30 are both multiples of 5, and their sum is 50, which is also a multiple of 5.

These properties and patterns can be useful when working with multiples of 5 in various mathematical calculations and problem-solving situations.

Applications of Multiples of 5

Multiples of 5 have various applications in everyday life. Here are some examples:

25: Multiples of 5 can be used to calculate percentages. For example, if you want to find 25% of a number, you can simply divide it by 4.

35: Multiples of 5 can also be used in time calculations. For instance, if you have 35 minutes, it is equivalent to 0.58 hours.

15: Multiples of 5 are useful in measuring angles. For instance, a 15-degree angle is one-third of a 45-degree angle.

40: Multiples of 5 are commonly used in temperature conversions. For example, 40 degrees Celsius is equivalent to 104 degrees Fahrenheit.

45: Multiples of 5 can be used in music theory. For instance, a 45 RPM record plays at 45 revolutions per minute.

30: Multiples of 5 are used in sports scoring. For example, in basketball, a team can score 30 points for a three-point shot.

10: Multiples of 5 are used in currency conversions. For instance, if the exchange rate is 10 to 1, then 10 units of one currency are equivalent to 1 unit of another currency.

20: Multiples of 5 are used in weight measurements. For example, 20 pounds is equivalent to 9.07 kilograms.

In conclusion, multiples of 5 have a wide range of applications in various fields, including mathematics, time, angles, temperature, music, sports, currency, and weight measurements.

Mathematical Operations

In the context of multiples of 5, understanding mathematical operations is essential. Multiples of 5 are numbers that can be divided evenly by 5. Let’s explore some common mathematical operations involving multiples of 5:

1. Addition: Adding multiples of 5 can be done by simply adding the numbers together. For example, 15 + 10 = 25. Similarly, 20 + 45 = 65.

2. Subtraction: Subtracting multiples of 5 involves subtracting the numbers from each other. For instance, 40 – 5 = 35. Likewise, 35 – 30 = 5.

3. Multiplication: Multiplying multiples of 5 can be done by multiplying the numbers together. For example, 5 x 8 = 40. Similarly, 5 x 7 = 35.

4. Division: Dividing multiples of 5 involves dividing the numbers by 5. For instance, 45 ÷ 5 = 9. Likewise, 30 ÷ 5 = 6.

Understanding these mathematical operations can help in various applications, such as calculating sums, differences, products, and quotients involving multiples of 5. It is important to practice these operations to enhance mathematical skills and problem-solving abilities.

Number Systems and Bases

In mathematics, a number system is a way of representing numbers using a set of symbols or digits. The most commonly used number system is the decimal system, which uses the base 10. This means that there are 10 possible digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

Another commonly used number system is the binary system, which uses the base 2. In the binary system, there are only two possible digits: 0 and 1. Each digit in a binary number represents a power of 2. For example, the binary number 1010 represents the decimal number 10.

The octal system uses the base 8 and has 8 possible digits: 0, 1, 2, 3, 4, 5, 6, and 7. Each digit in an octal number represents a power of 8. For example, the octal number 30 represents the decimal number 24.

The hexadecimal system uses the base 16 and has 16 possible digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Each digit in a hexadecimal number represents a power of 16. For example, the hexadecimal number 2D represents the decimal number 45.

Number systems and bases are used in various applications, such as computer programming, digital electronics, and cryptography. Understanding different number systems and bases is essential for working with these applications and solving problems related to them.

For example, in computer programming, the binary system is used to represent and manipulate data in computers. Each binary digit, also known as a bit, can represent either a 0 or a 1. By combining multiple bits, complex data can be represented and processed.

In digital electronics, number systems and bases are used to design and analyze circuits. Different number systems are used to represent different types of signals, such as analog and digital signals. Understanding number systems and bases is crucial for designing and troubleshooting electronic circuits.

In cryptography, number systems and bases are used to encrypt and decrypt messages. Different number systems and bases are used to represent and manipulate the data during the encryption and decryption process. Understanding number systems and bases is essential for implementing secure cryptographic algorithms.

In conclusion, number systems and bases are fundamental concepts in mathematics and have various applications in different fields. Understanding different number systems and bases is important for solving problems and working with applications related to these concepts.